Ứng dụng của toán trong đời sống săn sale
Giải thích công thức của thuật toán GETPERSPECTIVETRANSFORM và warpPerspective. Ứng dụng của toán học trong đời sống săn sale
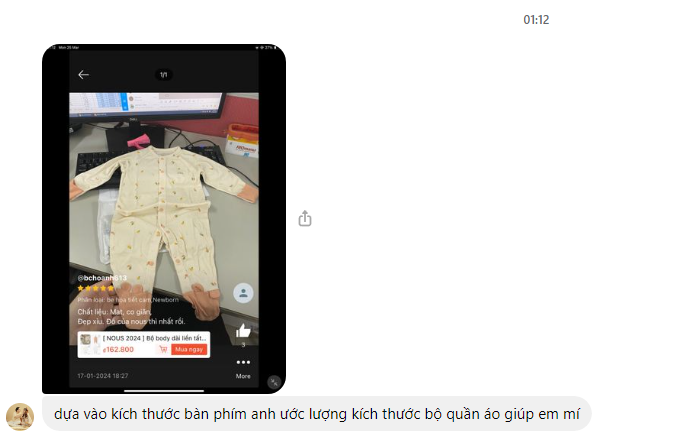
Hôm nay đang nằm ngủ lúc 1h sáng thì nhận được sin nhắn của vợ lúc săn sale. Mình cũng hốt hoảng vì tự nhiên vợ hỏi như vậy. Vậy thì bây giờ phải trả lời như nào ? Vừa nhanh vừa không phải dậy mở máy tính để viết công thức code ?
Bước 1: Mình nhìn kỹ thì con bàn phím đó là FUHLEN L411. Lên mạng tìm kiếm thì kích thước của nó là 45.1x14.2.3x3 (cm)
Bước 2: Lấy tọa độ và thông tin có trên hình:
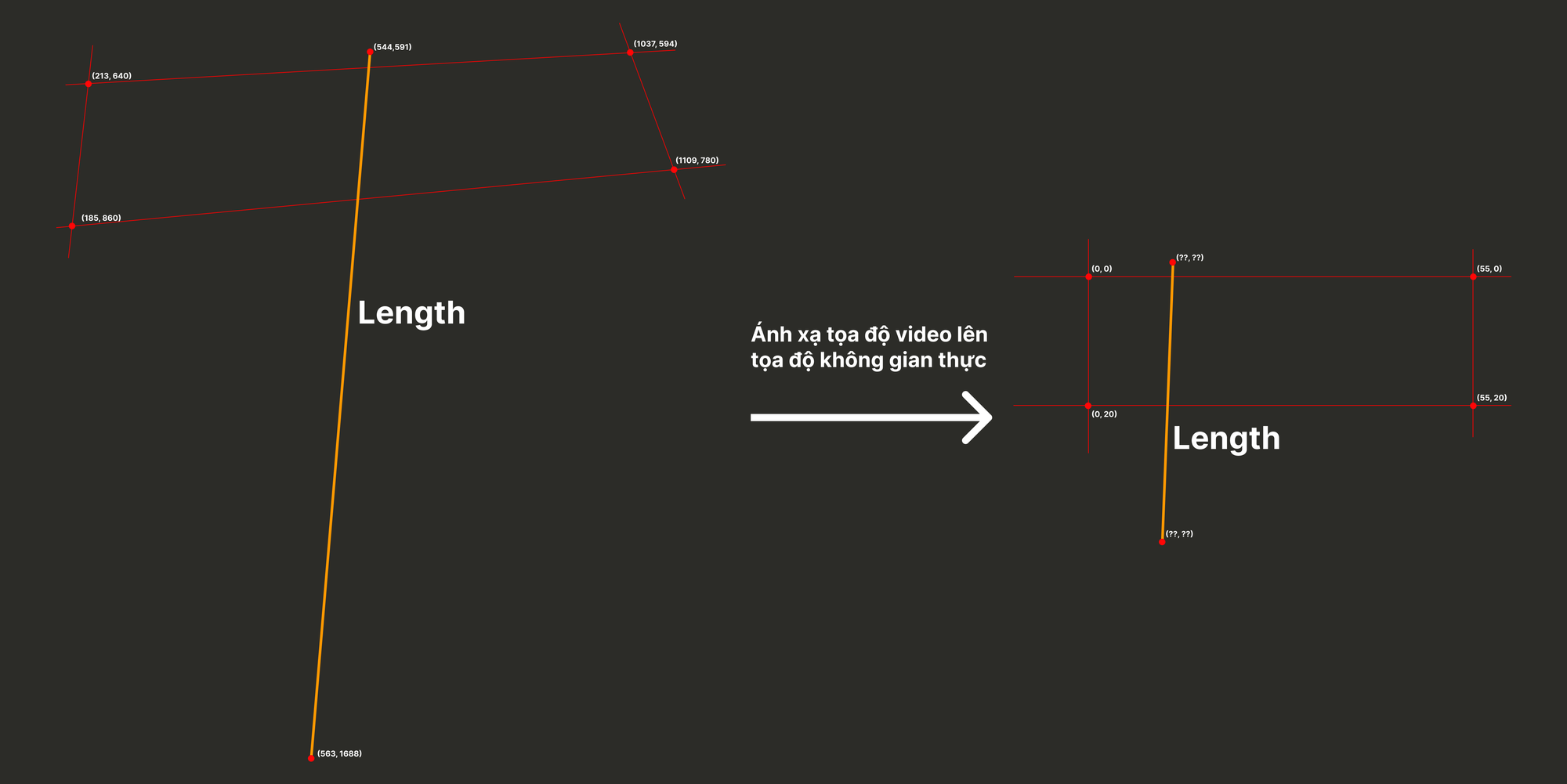
- Đường màu cam sẽ là khoảng cách mình cần tính
- Ngoài ra mình kiểm tra cạnh bàn có thẳng không để kiểm tra xem camera có hiện tượng "mắt cá" hay không (về mép hình ảnh bị uốn cong), thì may quá không bị.
- 4 góc trên bàn phí có tọa độ p1 = (213, 640), p2 = (1037, 594), p3 = (1109, 780), p4 = (185, 860)
- 2 điểm đầu và cuối của cái áo sẽ có tọa độ p5 = (544, 591), p6 = (563, 1688)

Nhưng khi này, từ 4 điểm của bàn phìm tìm được. Ta thấy đây không phải là một hình chữ nhật ?

Vấn đề ở đây là khi quay video thì tiktoker đã đặt góc Camera không phải góc thẳng đứng. Mà là góc nghiêng dẫn tới hình đã bị xoay đi một khoảng. So với kích thước thật.
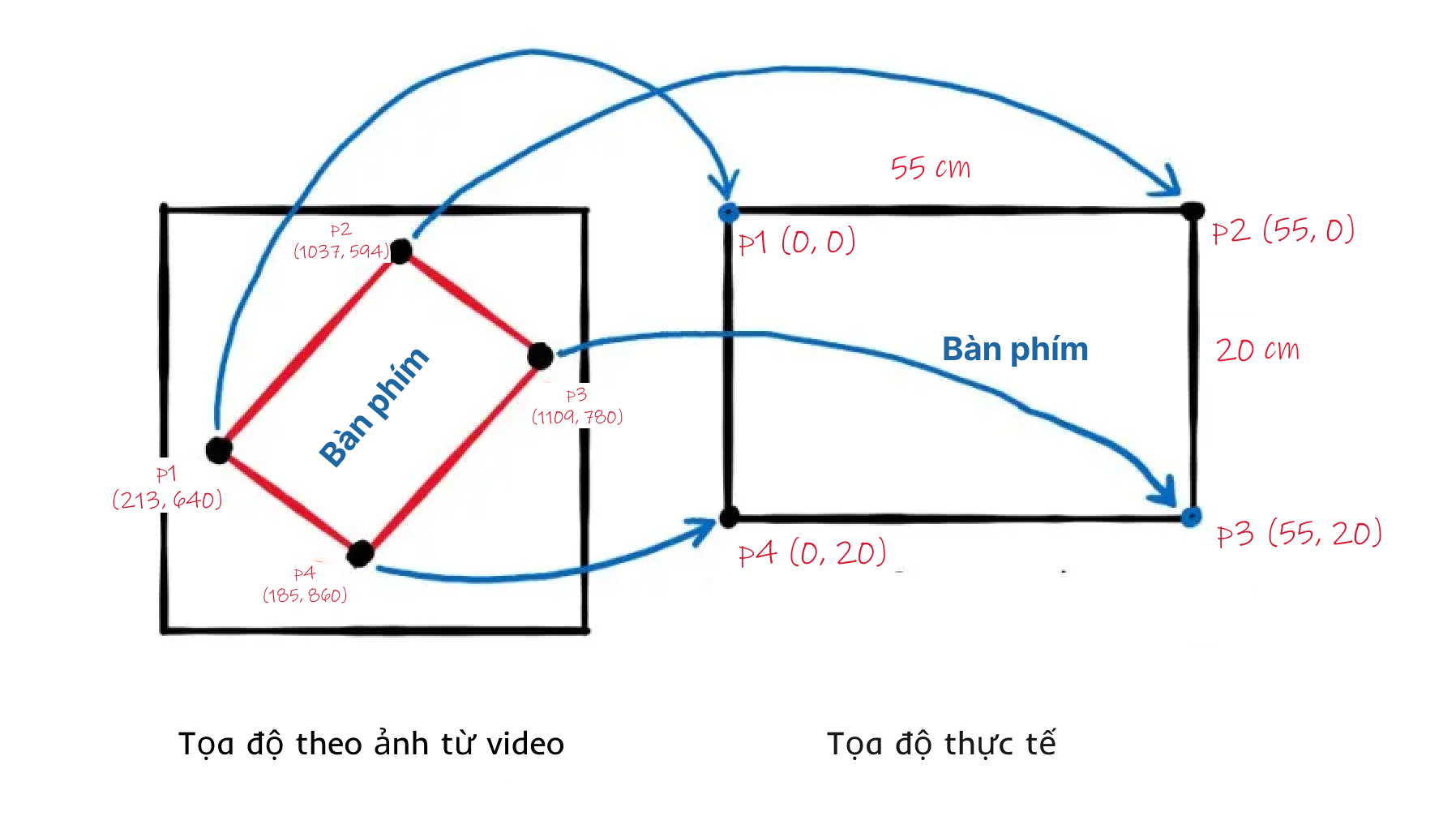
Bước 4: Tạo ma trận xoay tìm ánh xạ của kích thước thật của bàn phím trên ảnh.
Bài toán khi này sẽ có dạng như sau đây. Tìm ma trận ánh xạ để chuyển đổi tọa độ 4 điểm p1, p2, p3, p4 từ không gian của video về không gian thực tế. Sau đó sử dụng ma trận này tìm tọa độ điểm p5, p6 trên không gian thực tế
Giả định rằng tại không gian thực tếvới đơn vị là cm. Coi rằng điểm p1 nằm ở tọa độ \( p_1 = (0,0) cm \). Gọi ma trân tại đây là ma trận \( M \)
Ta có:
Với hệ tọa độ không gian 2 chiều với một chiều scaling thì Ma trận M sẽ có dạng là ma trận \( 3*3 \)
\[ M = \begin{bmatrix}a_1 & a_2 & a_3 \\ a_4&a_5&a_6 \\ a_7&a_8&a_9\end{bmatrix} \]
\[ \begin{bmatrix} x' \\ y' \\1\end{bmatrix} = M\times \begin{bmatrix} x \\ y \\ 1\end{bmatrix} =\begin{bmatrix}a_1x + a_2y + a_3 \\a_4x + a_5y + a_6 \\a_7x + a_8y + a_9\end{bmatrix}\\x, y: \text{Tọa độ trên không gian video}\\w':\text{Scaling trên không gian thực (cm)}\\x',y': \text{Tọa độ trên không gian thực}\\w=1:\text{Scaling trên không gian video (pixel)} \\M:\text{Ma trận chuyển đổi}\]
Để chuyển về tọa độ ảnh thực \(x',y'\), ta sử dụng công thức biến đổi
\[ x' = \frac{a_1x + a_2y + a_3}{a_7x + a_8y + a_9}\]
\[y' = \frac{a_4x + a_5y + a_6}{a_7x + a_8y + a_9} \]
Với một cặp điểm (in video - thực tế) ta sẽ có phương trình như trên.
Với 4 cặp điểm ứng với 4 góc của bàn phím \((x, y)\) và \((x', y')\), ta có thể thiết lập một hệ 8 phương trình tuyến tính để giải cho 9 ẩn \(a_1, a_2, \cdots a_9\).
Thể hiện tất cả các biến của hệ phương trình dưới dạng một ma trận A:
\[ A =\left[\begin{matrix}x_{1} & y_{1} & 1 & 0 & 0 & 0 & - x'_{1} x_{1} & - x'_{1} y_{1} & - x'_{1}\\x_{2} & y_{2} & 1 & 0 & 0 & 0 & - x'_{2} x_{2} & - x'_{2} y_{2} & - x'_{2}\\x_{3} & y_{3} & 1 & 0 & 0 & 0 & - x'_{3} x_{3} & - x'_{3} y_{3} & - x'_{3}\\x_{4} & y_{4} & 1 & 0 & 0 & 0 & - x'_{4} x_{4} & - x'_{4} y_{4} & - x'_{4}\\0 & 0 & 0 & x_{4} & y_{4} & 1 & - x_{4} y'_{4} & - y'_{4} y_{4} & - y'_{4}\\0 & 0 & 0 & x_{3} & y_{3} & 1 & - x_{3} y'_{3} & - y'_{3} y_{3} & - y'_{3}\\0 & 0 & 0 & x_{2} & y_{2} & 1 & - x_{2} y'_{2} & - y'_{2} y_{2} & - y'_{2}\\0 & 0 & 0 & x_{1} & y_{1} & 1 & - x_{1} y'_{1} & - y'_{1} y_{1} & - y'_{1}\end{matrix}\right] \]
"Tính nhẩm" theo phương pháp Gaussian Elimination hoặc Singular Value Decomposition để giải hệ phương trình thể hiện tại ma trận A
Ta tính được nghiệm của hệ phương trình
\[ M = \begin{bmatrix}0.0008 & 0.0001 & -0.2501 \\0.0001 & 0.0015 & -0.9682 \\-0.0000 & 0.0000 & 0.0092 \\\end{bmatrix}\]
Sau khi giải được hệ phương trình, ứng dụng công thức phía trên với tọa độ 2 điểm đầu và cuối của bộ quần áo đó được ban đầu ta có:
\[ x' = \frac{a_{1} x + a_{2} y + a_{3}}{a_{7} x + a_{8} y + a_{9}} \\ y'=\frac{a_{4} x + a_{5} y + a_{6}}{a_{7} x + a_{8} y + a_{9}} \]
Thay lần lượt từng điểm p5 = (544, 591), p6 = (563, 1688) vào công thức ta tính được tọa độ điểm trên không gian cm:
p5 = (16.87, -2.42)
p6 = (14.79, 49.92)
Vậy độ dài của chiếc áo sẽ là
\[ \text{length} =\sqrt{(16.87 - 14.79)^2 + (-2.42 - 49.92)^2} = 52.386 \ (cm)\]
Vậy là mình có thể trả lời vợ:
Kết luận:
Đây chỉ là một ví dụ vui về ứng dụng của toán học trong cuộc sống hàng ngày. Từ đây bạn có thể trả lời mấy ông hỏi "Học nhân ma trận để làm gì ? Chẳng có ứng dụng gì ..."
- Đây chỉ là một ứng dụng vui nhưng việc hiểu kỹ công thức cũng như thuật toán giúp bạn có thể tiến xa hơn và giải các bài toán phức tạp hơn mà thư viện không hỗ trợ:
- Giả sử bạn cần giải bài toán này trên một ngôn ngữ rất mới hoặc đơn giản là sử dụng SQL trực tiếp trên datalake để transform một loạt điểm từ dữ liệu GPS của người dùng chẳng hạn. Hoặc là ứng dụng onchain của blockchain ...
- Mặc dù đây là ví dụ với bài toán 2D. Nhưng cùng công thức này ta có thể mở rộng ứng dụng với bài toán 3D với các bản vẽ thiết kế, 4D với xử lý mô phỏng.
Một lần nữa, tôi không phủ nhận tính ứng dụng nhanh gọn của thư viện. Nhưng nếu chỉ dùng mà không hiểu sẽ gây lãng phí, không chắc chắn về kết quả, không khẳng định được tuyệt đối. Hãy tìm hiểu sâu hơn một vài layers nữa nhé, sẽ đưa bạn đi xa hơn trong nghề
Full code:




