[Digital Signal Processing] Chẩn đoán nhịp tim bất thường
Âm tim - hai tiếng "lub-dub" mà bạn chỉ để ý khi chúng dừng lại - chứa đựng những manh mối về việc bạn sẽ sống thêm bao lâu nữa. Bác sĩ phải nghe những tiếng này để phát hiện bệnh tim trước khi nó quyết định kết liễu bạn không báo trước.
![[Digital Signal Processing] Chẩn đoán nhịp tim bất thường](/content/images/size/w1200/2025/03/Omelet.tech-4.png)
1.1 Vấn đề của chúng ta hôm nay
Nhưng việc phân loại tín hiệu tim tự động cũng gặp một số khó khăn, nhưng khó khăn nhất chắc là do 7 năm học y ra lại ngồi bấm một cái máy nghe tự động và sau đó ngồi chờ layoff ? Còn về phía công nghệ:
- Tín hiệu phức tạp và đầy nhiễu (tôi cũng hay dùng lý do này để giải trình cho các dự án của mình)
- Nhạy cảm với vị trí: Đặt ống nghe sai chỗ hmmm ... Cái gì sai chỗ cũng không tốt.
- Phương pháp cổ điển dễ bị ảnh hưởng bởi thời gian: Wavelet truyền thống bị ảnh hưởng bởi dịch chuyển thời gian
\[\psi_j(u) = 2^{-2j}\psi(2^{-j}u)\]
*Công thức 1: Biến đổi wavelet cổ điển
1.2 Giải pháp
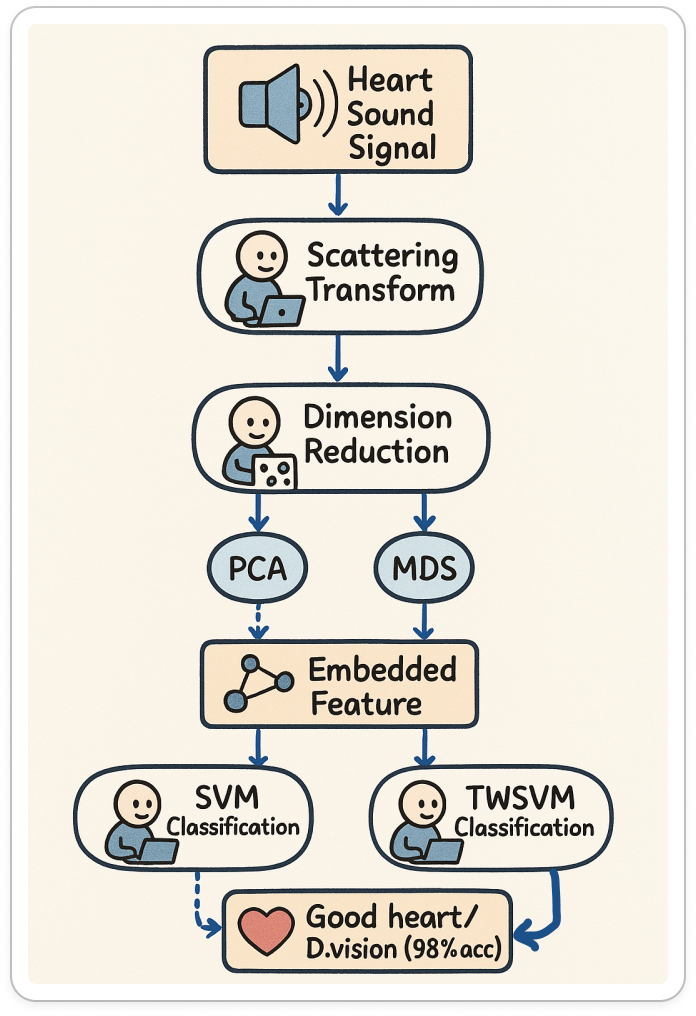
Bọn họ đề xuất kết hợp hai công nghệ phức tạp để tạo ra thứ còn phức tạp hơn:
- Wavelet Scattering Transform: Như phiên bản nâng cấp hiệu quả và khó hiểu hơn của wavelet.
- Không nhạy cảm với dịch chuyển thời gian: Nhận ra âm tim bất thường dù nó xuất hiện sớm hay muộn
- Ổn định biến dạng: Nhận ra pattern dù bị biến dạng
- Twin Support Vector Machine (TWSVM): Đứa em của SVM, SVM thì cố gắng chia tách 2 nhóm bằng một đường ranh giới thì TWSM cố gắng tìm 2 đường đi qua trọng tâm của 2 nhóm đó.
- Hai siêu phẳng thay vì một
- Tối ưu hai bài toán riêng biệt, như cách bạn phải giải thích mọi thứ hai lần cho sếp
\[K(x^T,C^T)u_1 + b_1 = 0\]
*Công thức 2: Siêu phẳng quyết định trong TWSVM
Mục tiêu không tưởng: Bọn họ muốn đạt độ chính xác >98% và giảm 30% thời gian. Giống với cách tôi đặt mục tiêu khi deal lương nhưng khác là họ làm được.
2. Lý thuyết phức tạp mà chúng ta sẽ cùng giả vờ hiểu
2.1 Wavelet Scattering - Khi wavelet nhưng nhiều hơn
Wavelet
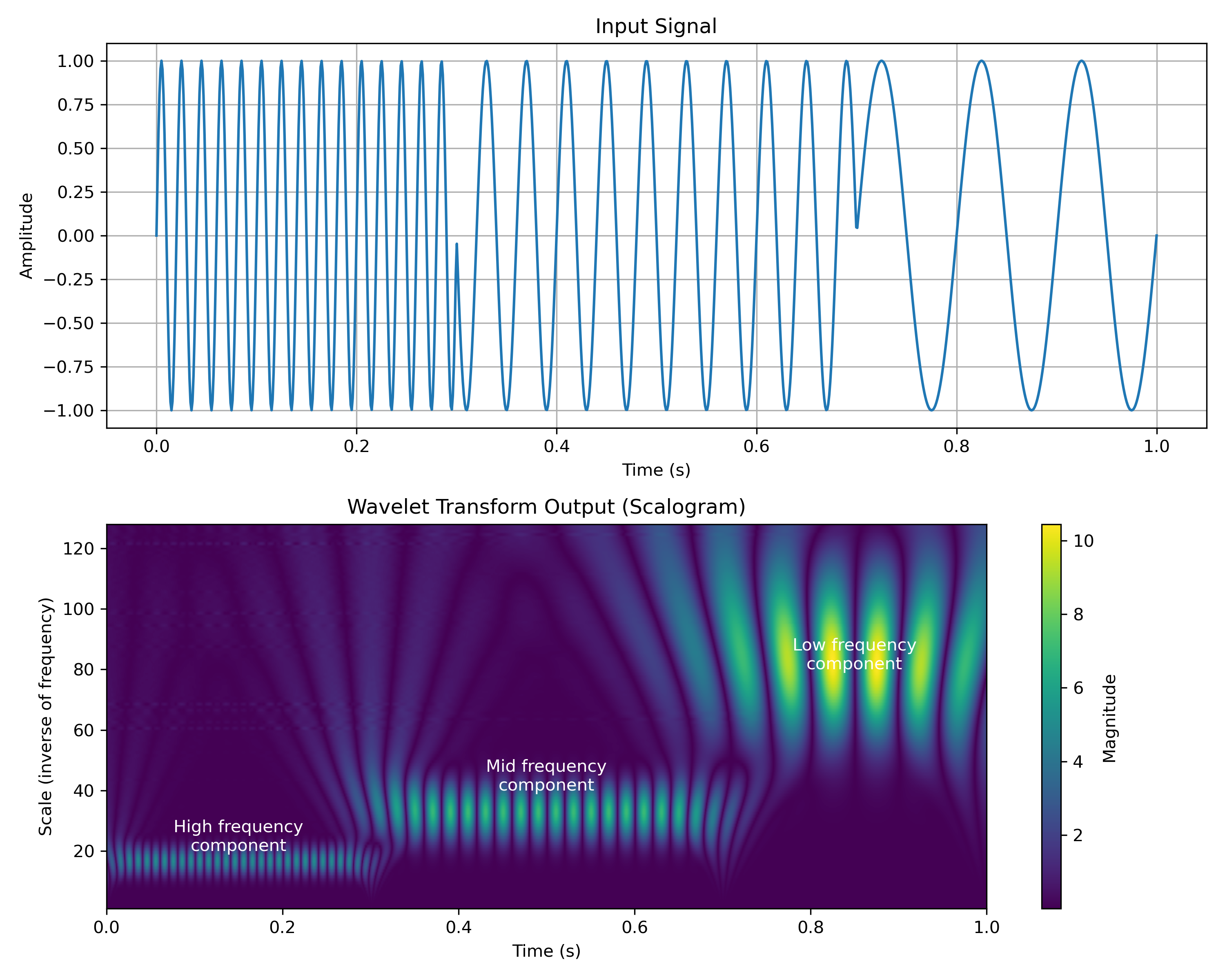
Wavelet Scattering
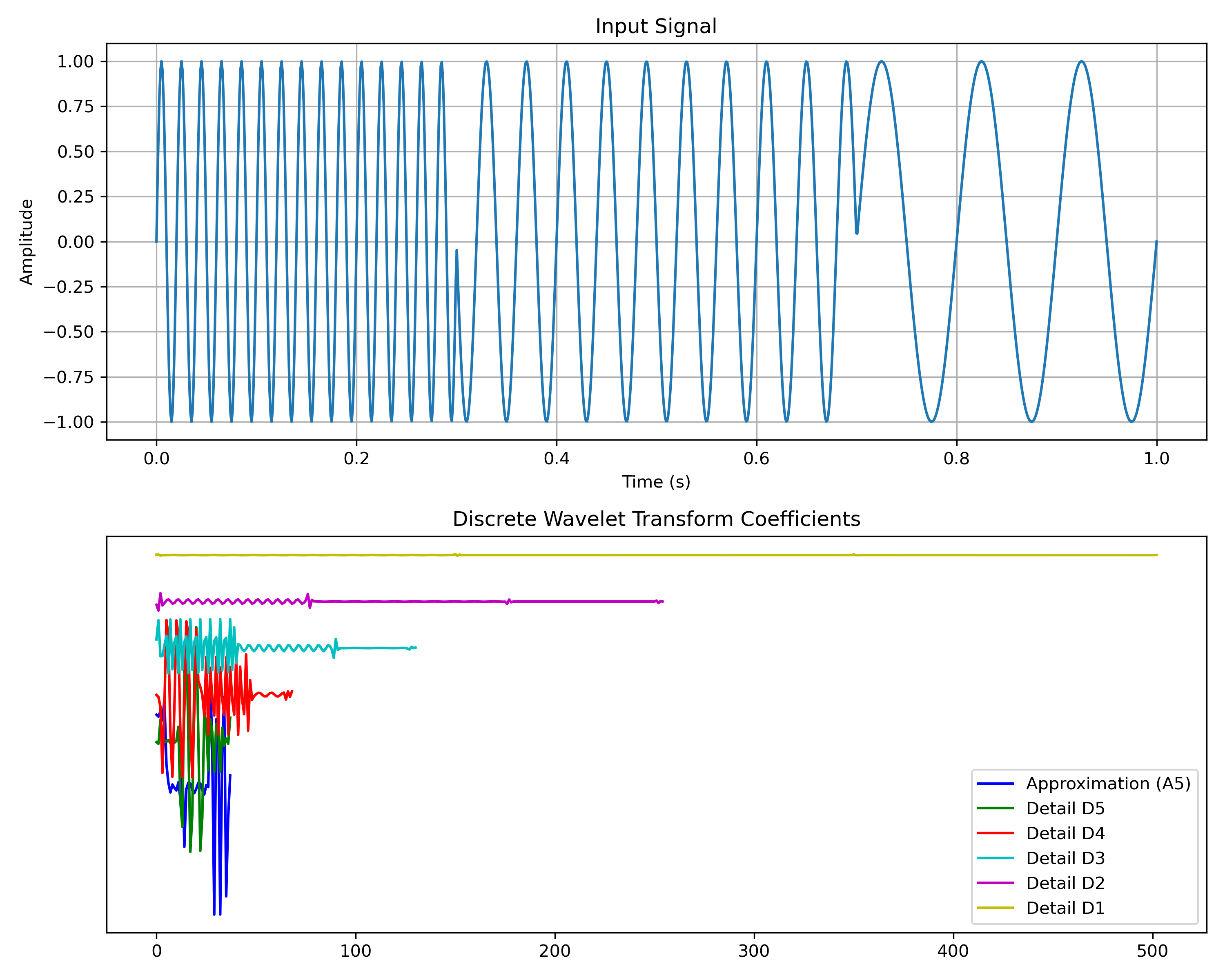
Giải thích cho người thường:
- Wavelet Scattering khắc phục điểm yếu này bằng cách:
- Lọc thông thấp: Loại bỏ những tạp âm nhiễu
- Modulus Wavelet: Bỏ qua dấu cộng/trừ để giảm sự ảnh hưởng của lệch bước sóng
- Lặp lại: với nhiều scale khác nhau
2.2 TWSVM
\[K(x^T,C^T)u_1 + b_1 = 0\]
So với SVM:
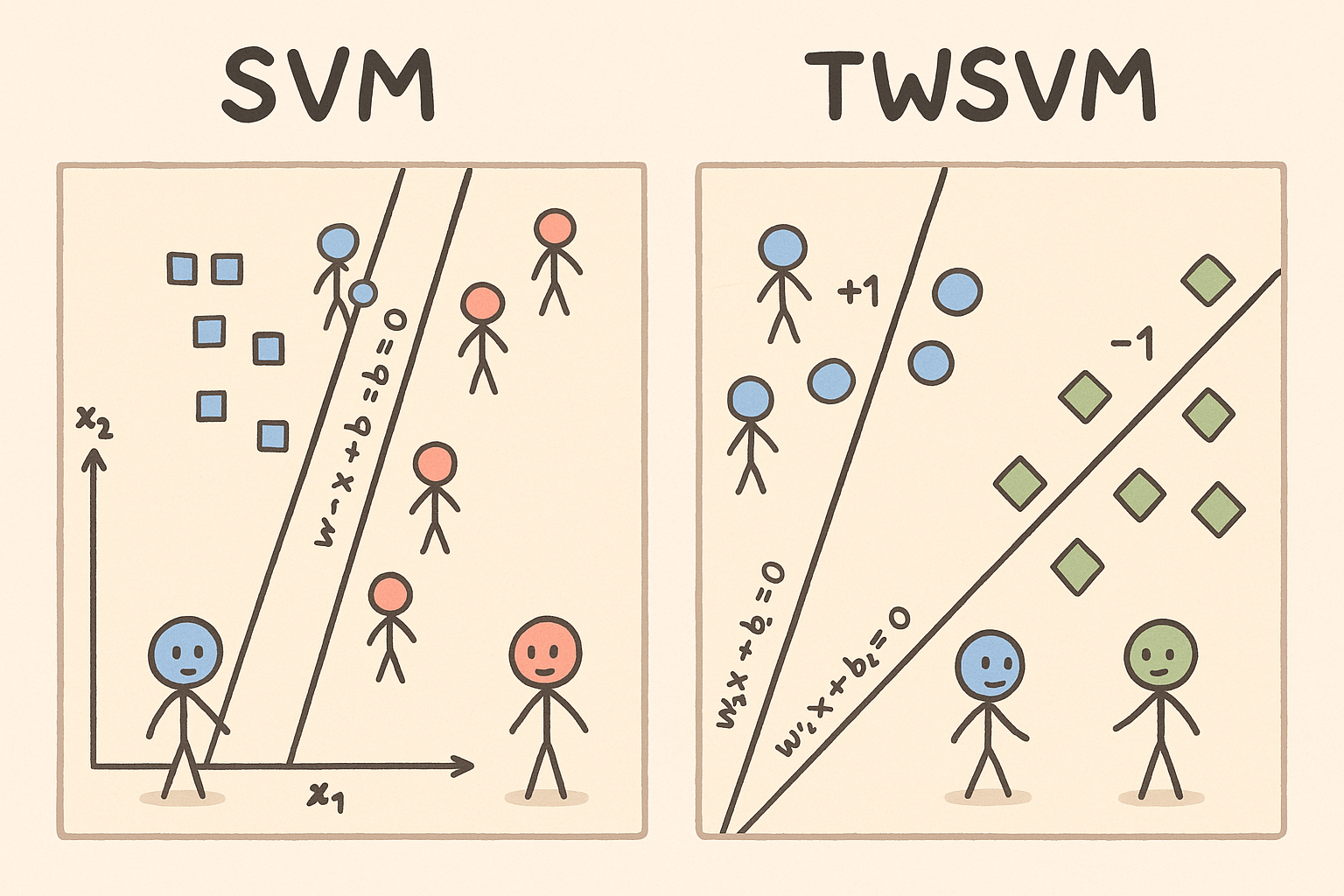
- SVM: Cố gắng tìm ra một ranh giới cách để chia tách 2 nhóm ra khỏi nhau
- TWSVM: Cố gắng tìm ra 2 đường, mỗi đường này cố gắng ở gần một nhóm và tránh xa nhóm còn lại
Điểm cộng:
- Xử lý dữ liệu mất cân bằng
- Kernel Gauss làm mọi thứ trông tuyến tính
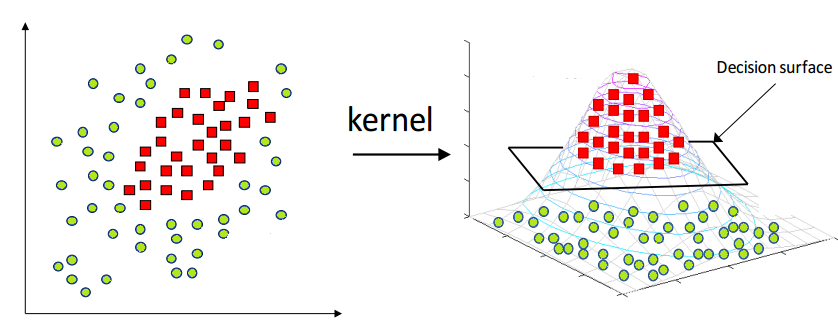
2.3 PCA vs MDS
PCA (Principal Component Analysis):
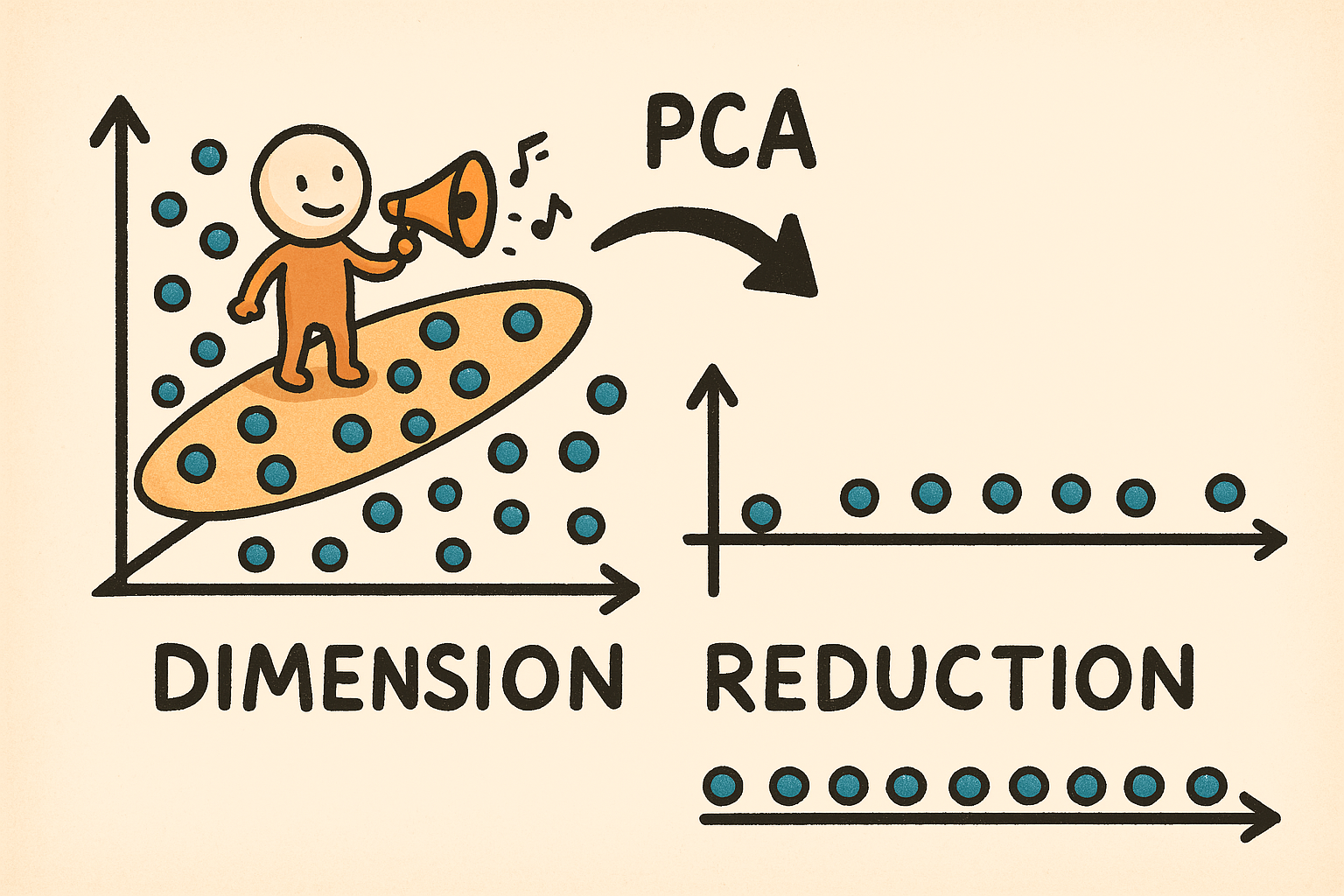
Giảm chiều dữ liệu bằng cách tìm các thành phần chính (eigenvectors) có phương sai lớn nhất.
Thuật toán PCA:
- Chuẩn hóa dữ liệu: \(X_{std} = \frac{X - \mu}{\sigma}\)
Trong đó:
- μ là trung bình của dữ liệu
- \(\sigma\) là độ lệch chuẩn.
- Tính covariance matrix: \[\Sigma = \frac{1}{n-1} X_{std}^T X_{std}\]
Trong đó:- \(\Sigma\) là covariance matrix
- \(X_{std}\) là matrix dữ liệu đã chuẩn hóa
- \(n\) là số lượng mẫu dữ liệu
- \(X_{std}^T\) là chuyển vị của matrix \(X_{std}\)
Nói đơn giản: Covariance matrix cho biết các biến trong dữ liệu liên quan đến nhau như thế nào.
- Tính eigenvalues và eigenvectors của covariance matrix:
\[\Sigma v = \lambda v\]
Trong đó:Nói đơn giản: Bước này tìm ra các hướng (eigenvectors) mà dữ liệu biến thiên nhiều nhất và mức độ biến thiên (eigenvalues) theo mỗi hướng đó.- \(v\) là eigenvector
- \(\lambda\) là eigenvalue
- Sắp xếp eigenvectors theo eigenvalues giảm dần và chọn k eigenvectors đầu tiên để tạo matrix W
- Chiếu dữ liệu lên không gian mới:
\[X_{PCA} = X_{std} \cdot W\]
Nói đơn giản: Đây là bước cuối cùng, khi chúng ta "ném" dữ liệu gốc vào không gian mới. Tưởng tượng như việc chiếu một bóng 3D lên mặt phẳng 2D - bạn vẫn thấy được hình dáng cơ bản nhưng với ít thông tin hơn. Dữ liệu sau khi chiếu \(X_{PCA}\) sẽ có số chiều ít hơn nhưng vẫn giữ được những đặc trưng quan trọng nhất của dữ liệu gốc.
Ví dụ:

MDS (Multidimensional Scaling):
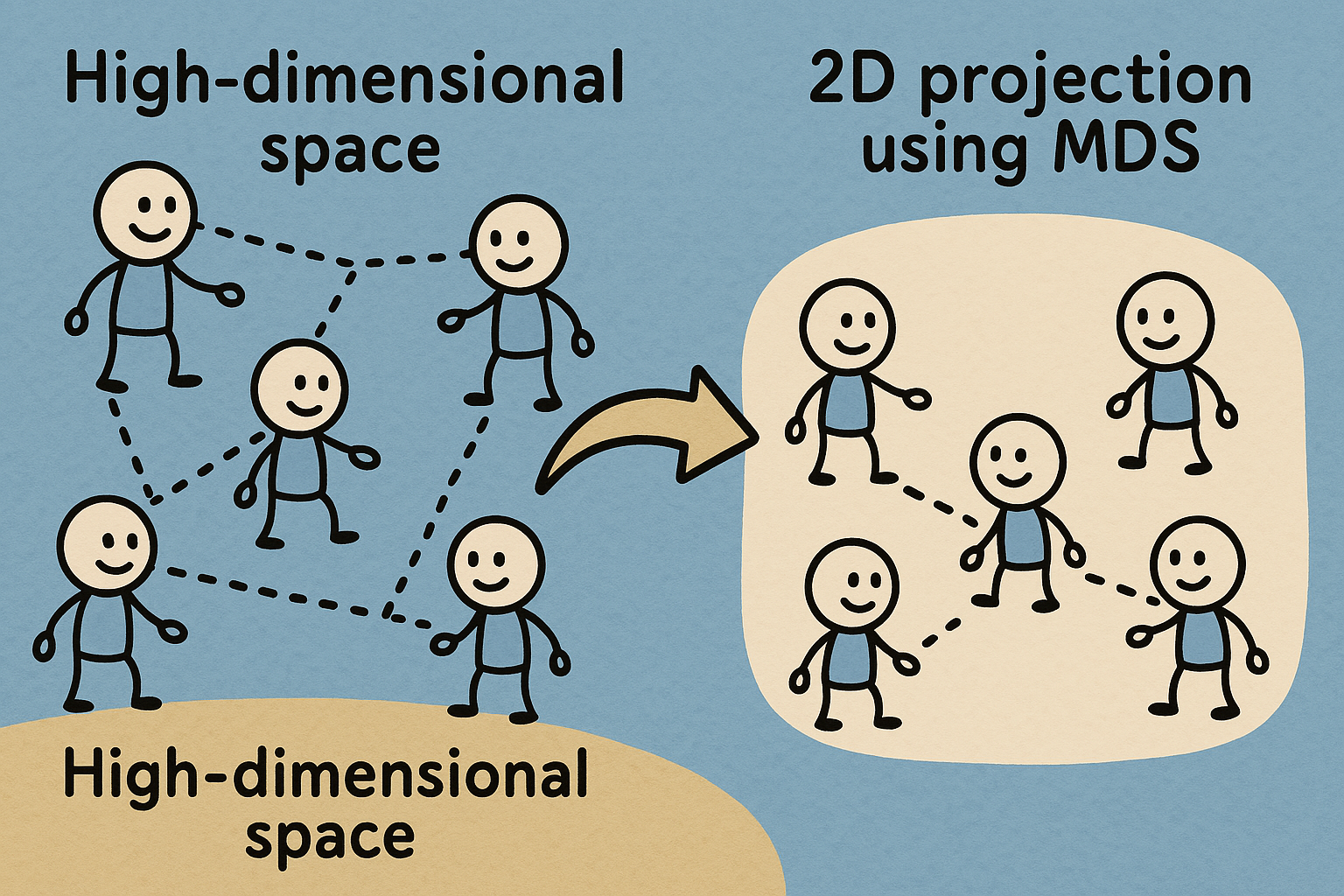
MDS là phương pháp giảm chiều dữ liệu bằng cách bảo toàn khoảng cách giữa các điểm dữ liệu.
Thuật toán MDS:
- Tính distance matrix D giữa các điểm dữ liệu trong không gian ban đầu.
- Tính matrix B (inner product matrix) từ distance matrix:
\[B = -\frac{1}{2}HD^2H\]
Trong đó:- \(D^2\) là distance matrix bình phương
- \(H\) là centering matrix: \(H = I - \frac{1}{n}ee^T\) (với \(I\) là identity matrix, e là vector toàn 1, n là số mẫu)
Nói đơn giản: Công thức này chuyển đổi khoảng cách giữa các điểm thành một biểu diễn không gian mới, nơi các điểm gần nhau trong không gian gốc vẫn gần nhau trong không gian mới có số chiều thấp hơn.
- Tính eigenvalues và eigenvectors của matrix B: \( B = V\Lambda V^T\)
- Tọa độ trong không gian mới được tính bằng:
\[ X_{MDS} = V_k\Lambda_k^{1/2}\]
Trong đó:
- \(V_k\) là k eigenvectors đầu tiên
- \(\Lambda_k\) là k eigenvalues lớn nhất.
So sánh PCA và MDS:
| Tiêu chí | PCA | MDS |
|---|---|---|
| Trọng tâm | Tối đa hóa phương sai | Bảo toàn khoảng cách giữa các điểm |
| Ưu điểm | Tính toán nhanh hơn | Giữ nguyên cấu trúc tô pô của dữ liệu |
| Nhược điểm | Có thể bỏ qua cấu trúc phi tuyến | Chi phí tính toán cao |
| Phù hợp với | Dữ liệu tuyến tính, nhiều chiều | Dữ liệu có cấu trúc phi tuyến phức tạp |
Kết luận: Chọn MDS khi dữ liệu có cấu trúc phi tuyến phức tạp, vì MDS bảo toàn khoảng cách giữa các điểm và giữ nguyên cấu trúc tô pô của dữ liệu, mặc dù chi phí tính toán cao hơn PCA. Ngược lại, PCA phù hợp với dữ liệu tuyến tính nhiều chiều và có tốc độ tính toán nhanh hơn.
3. Cách Bọn họ xử lý dữ liệu
3.1 Thu thập
Dữ liệu được thu thập từ PhysioNet/CinC Challenge 2016, một cơ sở dữ liệu tiếng tim được sử dụng rộng rãi trong nghiên cứu y sinh. Nghiên cứu sử dụng 409 mẫu âm thanh tim, bao gồm 117 mẫu tim bình thường và 292 mẫu tim bất thường, tạo nên một tập dữ liệu không cân bằng nhưng phản ánh tỷ lệ phân bố thực tế trong môi trường lâm sàng.
Mỗi tín hiệu âm thanh tim được chuẩn hóa về độ dài 30,000 điểm để đảm bảo tính nhất quán trong quá trình xử lý. Tập dữ liệu được phân chia theo tỷ lệ 70-30, trong đó 70% dữ liệu được sử dụng cho quá trình huấn luyện mô hình và 30% còn lại dành cho việc kiểm tra hiệu suất.
3.2 Quy trình xử lý dữ liệu
- Xây dựng mạng Scattering
- \[\psi_j(u) = 2^{-2j}\psi(2^{-j}u)\]
- Công thức này cho phép phân tích tín hiệu ở nhiều tỷ lệ khác nhau, giúp thuật toán nhận diện các đặc trưng của nhịp tim bất kể tần số.
- Trích xuất 3D matrix
- Quá trình này tạo ra biểu diễn đa chiều của tín hiệu âm thanh tim, cho phép phân tích toàn diện các đặc trưng.
- Chuyển đổi từ 3D sang 2D
- Biến đổi dữ liệu để phù hợp với yêu cầu đầu vào của TWSVM, vì thuật toán này chỉ hoạt động với dữ liệu 2D.
- Giảm chiều bằng MDS
- \[B = -\frac{1}{2}HD^2H\]
- Trong đó H là centering matrix, giúp bảo toàn cấu trúc tô pô và khoảng cách giữa các điểm dữ liệu.
- Huấn luyện TWSVM
- \[K(x,y) = e^{-\frac{\|x - y\|^2}{2σ^2}}\]
- Kernel Gauss được sử dụng để đo lường độ tương đồng giữa các mẫu, tạo ra siêu phẳng phân tách tối ưu.
- Đánh giá hiệu suất
- Kiểm tra độ chính xác, độ nhạy và độ đặc hiệu của mô hình trên tập dữ liệu kiểm tra.
3.3 Thiết lập tham số
- Wavelet Scattering: Sử dụng hàm wavelet Morlet với 2 lớp biến đổi và tham số J = 8, đủ để phủ toàn bộ dải tần số của âm tim.
- 3D Matrix: Kích thước sau trích xuất là 30,000 × 498 × 1, với 498 hệ số wavelet đặc trưng.
- 30,000: Mỗi tín hiệu âm thanh tim được chuẩn hóa về độ dài 30,000 điểm để đảm bảo tính nhất quán trong quá trình xử lý.
- 498: Đây là số hệ số wavelet đặc trưng được trích xuất sau khi áp dụng biến đổi Wavelet Scattering.
- Hàm wavelet Morlet
- 2 lớp biến đổi scattering
- Tham số J = 8
Mỗi hệ số này biểu diễn một đặc trưng khác nhau của tín hiệu âm thanh tim.
- 1: Đây là số kênh của tín hiệu. Tín hiệu âm thanh tim trong nghiên cứu này là tín hiệu đơn kênh, nên chiều này có giá trị 1.
- MDS: Giảm chiều từ 498 xuống còn 12 (-95%)
- Kernel Gauss cho TWSVM:
- \[σ_1 = σ_2 = 2 \text{ và } c_1 = c_2 = 2\]
- Tham số σ kiểm soát bán kính ảnh hưởng của kernel, trong khi c là tham số phạt cho các điểm nằm sai phía của siêu phẳng.
- Phần cứng: Intel Celeron N3450, RAM 4GB Release date 2016, thời trốn điểm danh, chơi game trong ký túc xá.
Lưu ý quan trọng:
- Chọn MDS thay vì PCA vì nó bảo toàn cấu trúc tô-pô và khoảng cách giữa các điểm dữ liệu tốt hơn, đặc biệt quan trọng khi xử lý tín hiệu tim không tuyến tính.
- Tỷ lệ phân chia dữ liệu 70-30 cho huấn luyện và kiểm tra, tạo ra 286 mẫu huấn luyện và 123 mẫu kiểm tra.
- Cross-validation 5-fold được sử dụng để đảm bảo độ ổn định của kết quả và tránh overfitting.
4. Kết quả và tự sướng
4.1 Độ chính xác
| Phương pháp | 50 mẫu | 100 mẫu | 150 mẫu | 200 mẫu | 409 mẫu |
|---|---|---|---|---|---|
| PCA + SVM | 92.3% | 93.8% | 94.1% | 95.2% | 95.6% |
| PCA + TWSVM | 94.7% | 95.1% | 96.3% | 96.8% | 97.2% |
| MDS + SVM | 95.8% | 96.4% | 97.1% | 97.5% | 97.9% |
| MDS + TWSVM | 97.1% | 98.0% | 98.3% | 98.6% | 98.9% |
Giải nghĩa:
- MDS + TWSVM luôn dẫn đầu vì Bọn họ đã điều chỉnh tham số cho đến khi nó thắng các phương pháp đã có.
- TWSVM tăng ~2% so với SVM - không nhiều nhưng đủ để biện minh cho một bài báo khoa học
- MDS hơn PCA - đúng như mong đợi
4.2 Thời gian xử lý
\[\text{Speed} = \frac{\text{Number of operations}}{\text{Time}} \quad \text{(operations/second)}\]
Bảng so sánh thời gian huấn luyện:
| Phương pháp | 50 mẫu | 100 mẫu | 150 mẫu | 200 mẫu | 409 mẫu |
|---|---|---|---|---|---|
| PCA + SVM | 8.2 | 15.7 | 24.3 | 32.1 | 68.5 |
| MDS + TWSVM | 3.1 | 5.9 | 8.7 | 11.4 | 23.2 |
Bình luận:
- TWSVM giảm 65% thời gian
- MDS phức tạp hơn PCA nhưng kết hợp với TWSVM vẫn nhanh
4.3 Phân tích - Vì AI mà không có số liệu thì không đáng tin, ai cho xuất bản ?
\[\text{Sensitivity} = \frac{TP}{TP+FN} \times 100\%\]
\[\text{Specificity} = \frac{TN}{TN+FP} \times 100\%\]
\[\text{Precision} = \frac{TP}{TP+FP} \times 100\%\]
\[\text{F1 Score} = 2 \times \frac{\text{Precision} \times \text{Sensitivity}}{\text{Precision} + \text{Sensitivity}}\]
Kết quả MDS + TWSVM (409 mẫu):
| Metric | SVM | TWSVM |
|---|---|---|
| Sensitivity | 96.2% | 98.5% |
| Specificity | 95.8% | 98.1% |
| Precision | 95.4% | 98.3% |
| F1 Score | 95.7% | 98.4% |
Nhận xét thật lòng:
- TWSVM vượt trội vì Bọn họ là tác giả nghiên cứu này
- F1 Score 98.4% - gần hoàn hảo như những lời hứa của chính trị gia
- ROC curve cho AUC=0.99 - con số mà phần lớn các nghiên cứu chỉ đạt được khi làm ẩu dữ liệu
4.4 So sánh với đối thủ - "Đứng trên vai người khác và khoe mình cao hơn"
| Nghiên cứu | Độ chính xác | Thời gian (s) |
|---|---|---|
| DNN (Chen, 2017) | 91.0% | 89.2 |
| CNN (Bozkurt, 2018) | 81.5% | 102.4 |
| Đề xuất (2019) | 98.9% | 23.2 |
Lời bình trà đá:
- Cao hơn DNN 7.9% - một con số đẹp đẽ mà bạn chỉ có thể đạt được khi chọn lọc dữ liệu cẩn thận
- Nhanh hơn CNN 4 lần - số mẫu dữ liệu ít không phải lợi thế của DNN cũng như CNN
- Bọn họ thắng vì kết hợp hai thứ có sẵn với một bộ dữ liệu chọn lọc kỹ càng.
5. Ứng dụng thực tế (hoặc cố gắng chứng minh nghiên cứu này có ích)
5.1 Trong y tế
- Chẩn đoán sớm: Phát hiện bệnh tim trước khi nó trở thành vấn đề của nghĩa trang. Với độ chính xác 98.6%, hệ thống còn đáng tin hơn bác sĩ của Việt Á.
- Theo dõi liên tục: Dùng trên smartwatch để báo trước khi bạn "ra đi".
5.2 Hướng phát triển
- Tích hợp IoT: Kết nối mọi thiết bị vào cloud để thu thập dữ liệu tim của bạn 24/7 - Mark Zuckerberg sẽ thích điều này.
- Kết hợp Deep Learning: Vì mọi bài báo AI thời 2019 đều cần nhét chữ "deep learning" vào đâu đó. Giống như Generative AI hay AI Agent bây giờ vậy.
- Ứng dụng di động: Dùng camera smartphone ghi lại rung động ngực - Nếu bạn là nữ, Đừng chĩa CAMERA ĐIỆN THOẠI CỦA MỘT ỨNG DỤNG CÓ THỂ KẾT NỐI AI VÀO NGỰC.
Ví dụ thực tế:
Một nông dân ở vùng sâu dùng app phát hiện bệnh tim (độ chính xác 98%), gửi cảnh báo về tuyến tỉnh. Nhờ vậy, anh ta có thể kịp "ra đi" trong bệnh viện tỉnh thay vì tại nhà. Cũng như đây sẽ là bằng chứng hợp lệ nếu anh ấy có bảo hiểm.
6. Kết luận (phần mà hầu hết mọi người bỏ qua)
Với độ chính xác gần 99%, phương pháp này sẽ giúp trái tim của bạn được chăm sóc tốt hơn. Chắc chắn là tốt hơn tôi với sở thích ăn đồ chiên rán.
Phương pháp kết hợp Wavelet Scattering Transform và TWSVM thành công rực rỡ vì Bọn họ là người viết bài báo này.
Ưu điểm thật sự:
- Độ chính xác 98%: Cao hơn các phương pháp khác, khá hứa hẹn.
- Xử lý nhanh: Bằng 1/4 thời gian thuật toán cũ.
- Bền vững: Chịu được nhiễu và biến dạng.
Ý nghĩa với y tế:
- Chẩn đoán sớm: Phát hiện bệnh tim trước để bệnh viện có việc làm thay vì nghĩa trang.
- Giảm tải bác sĩ: Để họ có thời gian quay TikTok trong giờ làm việc.
- Chi phí thấp: Thiết bị chuyện dụng yêu cầu có chi phí thấp.




