Python

Các Metrics trong Bài toán Hồi quy (Regression)

Các Metrics trong Bài toán Hồi quy (Regression)

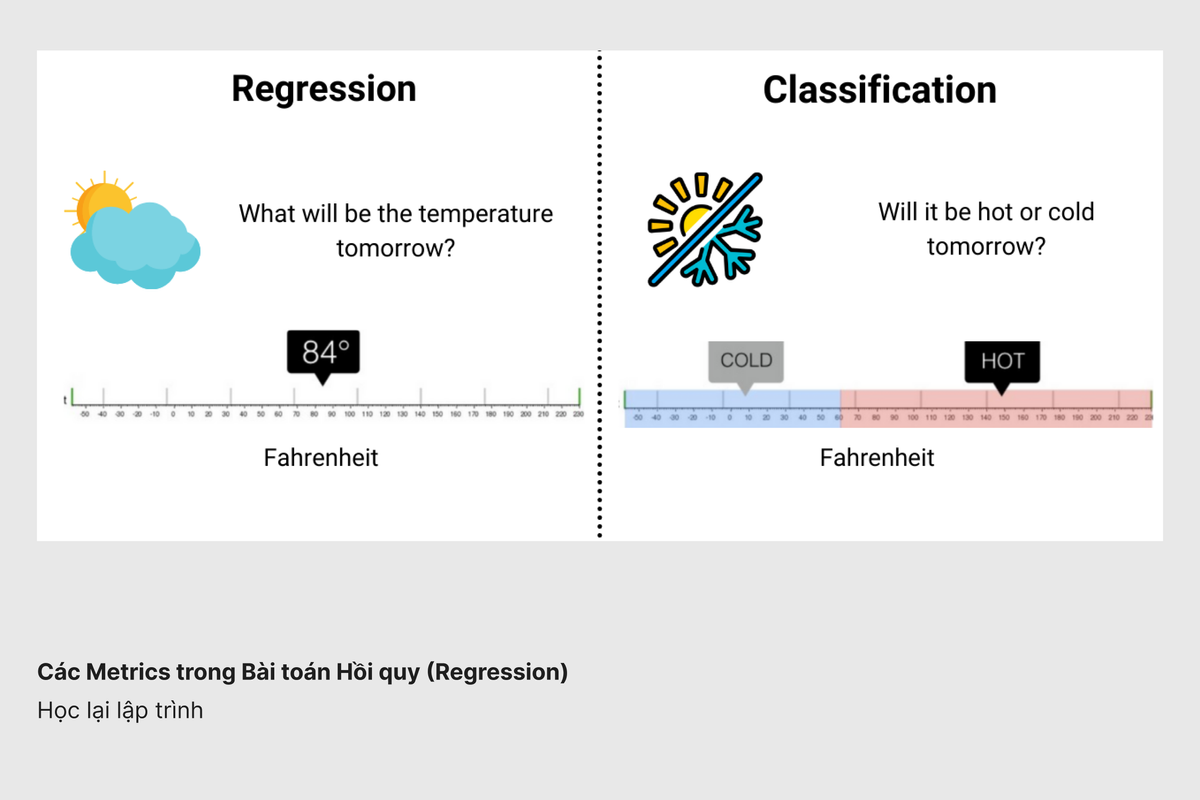
Tiếp tục theo sau bài viết về các metrics trong bài toán phân loại, hôm nay chúng ta tới với các metrics trong bài toán hồi quy (Regression).
Bài toán hồi quy là dạng bài toán mà output của mô hình không phải là một class mà sẽ là một giá trị nằm trong một khoảng liên tục.

AI_Part_3_Regression vs Classification Models
Ví dụ về bài toán Regression so với classification

Các ứng dụng của bài toán regression

1. Mean Absolute Error (MAE):

MAE là một trong những metrics đơn giản và trực quan nhất, phản ánh trung bình độ lệch tuyệt đối giữa giá trị dự đoán và giá trị thực tế. MAE cung cấp một cái nhìn không thiên vị về sai số trung bình mà mô hình của bạn tạo ra, giúp bạn đánh giá chất lượng dự đoán trong các tình huống thực tế.

Với định nghĩa trên thì cách hiểu MAE hết sức đơn giản. Ví dụ:

  • Nếu ta có giá trị thực tế là 3 và giá trị dự đoán là 5, sai số tuyệt đối sẽ là \(|3 - 5| = 2\). Tương tự, nếu ta dự đoán giá trị là 7 trong khi giá trị thực tế là 10, sai số tuyệt đối sẽ là \(|7 - 10| = 3\). MAE sẽ lấy trung bình của tất cả các sai số tuyệt đối như vậy.

Công thức:

\[ MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| \]

Sample Code

np.mean(np.abs(y_true - y_pred))

Đặc điểm:

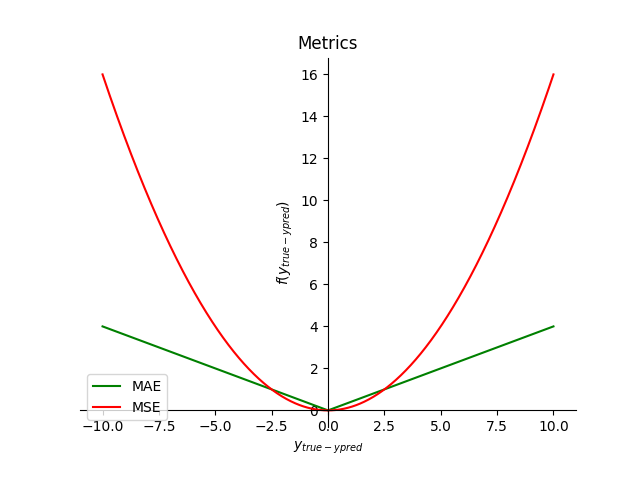
  • Trực quan, dễ hiểu. Không làm nổi bật các các sai số lớn.
  • MAE là metrics mà bạn muốn lựa chọn khi mà bạn muốn dự đoán sai số trung bình mà không quan tâm đến việc nó có phải là sai số lớn hay không.

2. Mean Squared Error (MSE):

MSE là trung bình của bình phương sai số giữa dự đoán và thực tế. Công thức này đặc biệt hữu ích khi bạn cần đặt trọng số nhiều hơn vào các sai số lớn, vì việc bình phương sẽ làm tăng sự chênh lệch của các sai số lớn so với sai số nhỏ.

Với định nghĩa trên thì ta có thể hiểu MSE đơn giản như sau:

  • Nếu ta có giá trị thực tế là 3 và giá trị dự đoán là 5, sai số bình phương sẽ là \((3 - 5)^2 = 4\). Tương tự, nếu ta dự đoán giá trị là 7 trong khi giá trị thực tế là 10, sai số bình phương sẽ là \((7 - 10)^2 = 9\). MSE sẽ lấy trung bình của tất cả các sai số bình phương như vậy.

Công thức:

\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]

Đặc điểm:

  • MSE là chỉ số mà bạn nên lựa chọn khi bạn muốn nhấn mạnh các sai số lớn. Điều này giúp làm nổi bật các điểm dữ liệu ngoại lai.
Mô tả sự khác biến đổi dữ liệu giữa nhau giữa MAE và MSE

3. Root Mean Squared Error (RMSE)

RMSE là một biến thể của MSE, cung cấp một cái nhìn trực quan hơn về sai số trung bình bằng cách lấy căn bậc hai của MSE. Điều này giúp RMSE trở lại cùng đơn vị đo lường với dữ liệu gốc, làm cho việc giải thích kết quả trở nên dễ dàng hơn.

Công thức:

\[ RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} \]

Sample Code:

((y_true - y_pred) ** 2).mean() ** 0.5

Đặc điểm:

  • Mang đặc điểm giống với MSE nhưng đã được chuyển về đơn vị cùng với đơn vị đo lường với dữ liệu gốc.

4. R-squared (R²)

R², còn được gọi là hệ số xác định (coefficient of determination), đo lường tỷ lệ phần trăm sự biến thiên của features mà mô hình hồi quy có thể thích ứng.

Ví dụ, một R² là 60% cho thấy 60% sự biến thiên của feature output (y) quan sát được trong tập dữ liệu được mô hình hồi quy thích ứng. Nói chung, một R² cao hơn chỉ ra rằng mô thích ứng được nhiều sự biến thiên ở output hơn.

Tuy nhiên, một giá trị R² cao không nhất thiết đồng nghĩa với một mô hình tốt, đặc biệt khi dữ liệu có chứa nhiễu.

Công thức

\[ R² = 1 - \frac{SS_{res}}{SS_{tot}} \]

trong đó \(SS_{res}\) là tổng bình phương sai số (sum of squared residuals) và \(SS_{tot}\) là tổng bình phương tổng (total sum of squares).

ss_res = ((y_true - y_pred) ** 2).sum()
ss_tot = ((y_true - y_true.mean()) ** 2).sum()
return 1 - (ss_res / ss_tot)

Đặc điểm:

  • R² chỉ ra phần trăm biến thiên của các đặc trưng đầu ra được thích ứng trong mô hình.
  • Một giá trị R² cao chỉ ra rằng mô hình có khả năng giải thích tốt dữ liệu. Tuy nhiên, R² không thể hiện được mức độ chính xác cụ thể của các dự đoán.

Kêt luận

Ngoài ra còn các metrics khác như MAPE, MSLE, … mà các bạn có thể tham khảo để lựa chọn được metrics phù hợp với mô hình của mình.

Mỗi metrics sẽ là một góc nhìn của bạn nhìn vào tương quan kết quả predict của model so với kết quả thực tế. Từ góc nhìn đó bạn có thể gián tiếp đánh giá độ “tốt” của model. Do đó tùy vào bài toán và bộ dữ liệu cụ thể mà bạn cần xem xét và áp dụng những metrics phù hợp. Điều quan trọng là đảm bảo rằng metrics bạn chọn thực sự phản ánh mục tiêu của dự án và giúp cải thiện hiệu suất của mô hình.

Read more