machine learning

Các metrics trong bài toán phân loại (Classification)

Các phép đo cơ bản trong bài toán Binary Classification

Các metrics trong bài toán phân loại (Classification)
Các metrics trong bài toán phân loại (Classification)

Trong quá trình làm việc và tham gia các cuộc phỏng vấn gần đây, tôi nhận thấy một xu hướng đáng chú ý: nhiều bạn trẻ ngày nay lao thẳng vào lĩnh vực công nghệ, đặc biệt là trí tuệ nhân tạo (AI) và học sâu (Deep Learning), mà không chú trọng đến những kiến thức nền tảng như Software Engineering hay Toán học cơ bản. Sự thiếu hụt này dẫn đến nhiều khó khăn trong cả quá trình làm việc lẫn phỏng vấn. Đây chính là lý do tôi quyết định viết loạt bài này, nhằm giúp mọi người ôn lại và nắm vững các khái niệm cơ bản của Machine Learning và Deep Learning.

Các công thức phổ biến trong bài toán phân loại (Classification)

Confusion Metric:

Đây là metric cơ bản mà chúng ta sẽ gặp trong các bài toán classification. Tại metric này ta cần hiểu được 4 chỉ số:

  • TP : True Positive. Label positive, predict positive - Kết quả đúng
  • TN : True Negative. Label negative, predict negative - Kết quả đúng
  • FP : False Positive. Label Negative nhưng dự đoán là Positive - Kết quả sai
  • FN: False Negative. Label Positive nhưng dự đoán là Negative - Kết quả sai

Công thức:

\[ \text{TP} = \sum_{i=1}^{N} 1(y_i = 1 , \text{and} , \hat{y}_i = 1) \]

\[ \text{TN} = \sum_{i=1}^{N} 1(y_i = 0 , \text{and} , \hat{y}_i = 0) \]

\[ \text{FP} = \sum_{i=1}^{N} 1(y_i = 0 , \text{and} , \hat{y}_i = 1) \]

\[ \text{FN} = \sum_{i=1}^{N} 1(y_i = 1 , \text{and} , \hat{y}_i = 0) \]

Accuracy (Độ chính xác)

Giải nghĩa: Tỉ lệ số lượng dự đoán đúng trên tổng số lượng dự đoán.

Công thức:

\[ \begin{aligned} \text{Accuracy} = \frac{1}{N} \sum_{i=1}^{N} 1(y_i = \hat{y}_i) = \frac{TP + TN}{TP + TN + FP + FN} \\ N = \text{Số lượng mẫu thử}\end{aligned} \]

Sample Code

(y_true == y_pred).mean()

Đặc điểm:

  • Dễ hiểu, trực quan nhưng không phù hợp với dữ liệu mất cân bằng.
    • VD: khi tập dữ liệu có 99% class là 1, 1% là 0. Khi này model chỉ cần dự đoán toàn bộ là 1 thì model sẽ có accuracy là 99%

Precision (Độ chắc chắn)

Tỉ lệ số lượng dự đoán đúng tích cực trên tổng số dự đoán tích cực. Ngắn gọn các bạn có thể nhớ là "số đoán đúng trên số đoán là đúng"

Công thức:

\[ \text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} \]

Sample code:

tp / (tp + fp)

Đặc điểm:

  • Precision sẽ là metric để kiểm tra độ chắc chắn trong dự đoán của model.
  • Ví dụ bài toán ưu tiên Precision:
    • Bài toán phát hiện gian lận và tự chặn giao dịch từ thẻ của người dùng. Trong bài toán này để đảm bảo không gây ra các bất tiện trong quá trình giao dịch của người dùng. Hệ thống cần ưu tiên độ chắc chắn của mô hình khi đưa ra quyết định.

Recall (Độ phủ)

Tỉ lệ số lượng dự đoán đúng tích cực trên tổng số trường hợp thực sự đúng. Các bạn có thể nhớ ngắn gọn là "Số đoán đúng trên số phải đoán"

Công thức:

\[ \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} \]

Sample Code:

tp / (tp + fn)

Đặc điểm:

  • Recall sẽ là metric để kiểm tra độ phủ, độ nhạy cảm trong dự đoán của model.
  • Ví dụ bài toán ưu tiên Recall:
    • Bài toán trong chuẩn đoán bệnh, cần ưu tiên độ nhạy cảm rất cao. Chỉ cần chớm có tín hiệu có bệnh thì cần cảnh báo để bệnh nhân đi thực hiện thêm các sét nghiệm kiểm tra.

F1 Score

Điểm sốtổng hòa giữa Precision và Recall, cung cấp một cái nhìn tổng quát về hiệu suất của mô hình.

Công thức

\[ F1 = 2 \times \frac{P \times R}{P + R} \\ P = \text{Precision} \\ R = \text{Recall} \]

Sample Code:

2 * (p * r) / (p + r)

ROC Curve (Đường cong ROC)

ROC Curve là một đồ thị biểu diễn khả năng phân biệt của một mô hình phân loại ở các ngưỡng quyết định (threshold) khác nhau. Đường cong này thể hiện mối quan hệ giữa Tỉ lệ Dương tính Giả (FPR - False Positive Rate) và Tỉ lệ Dương tính Thực (TPR - True Positive Rate), hay còn gọi là Recall, khi ngưỡng phân loại được thay đổi. ROC Curve sẽ được dùng để đánh giá và chọn Threshold cho bài toán phân loại.

Công thức:

\[ TPR=\frac{TP}{TP+FN} \]

\[ FPR=\frac{FP}{FP+TN} \]

Sample Code:

fpr, tpr, thresholds = metrics.roc_curve(y_true, y_scores)

Đặc điểm:

  • ROC Curve cung cấp một đánh giá toàn diện về hiệu suất của mô hình trên tất cả các thresholds.

AUC (Area Under the Curve)

AUC, viết tắt của "Area Under the Curve" (Diện tích dưới ROC Curve), là một chỉ số đo lường hiệu suất tổng thể của mô hình phân loại.
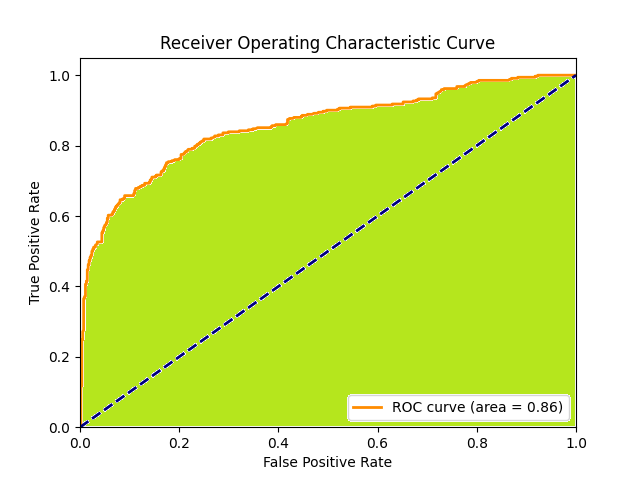
ROC Curve thể hiện kết quả trên một đồ thị được plot. Và AUC là tỷ lệ diện tích phần bên dưới của đồ thị đó so với tổng diện tích đồ thị. Khi này giá trị của AUC sẽ là một số, từ đó ta có thể dễ dàng quan sát và đánh giá trong quá trình training model.

Với hình dưới đây thì AUC. AUC sẽ là

\[ AUC=\frac{\text{diện tích màu xanh}}{\text{diện tích màu xanh} +\text{diện tích màu trắng}} \]

Sample code:

auc = metrics.roc_auc_score(y_true, y_pred)

Đặc điểm:

  • AUC là một thể hiện khác về diện tích của ROC. Do đó nó mang đầy đủ đặc điểm của ROC. Nhưng nó sẽ dễ dàng quan sát hơn trong quá trình training.

Read more